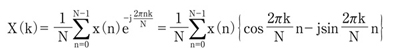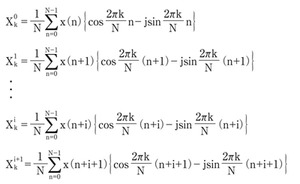安価なFPGAを利用可能なフーリエ変換回路:Design Ideas
一般に、フーリエ変換は、取得したデータに対してFFT(高速フーリエ変換)処理を施すことで行われる。しかし、例えばFPGAを用いてリアルタイムでFFT処理を行おうとすると、FFT用の回路を自作する場合でも、FPGAベンダー各社が提供するIP(Intellectual Property)を使用する場合でも、多くの回路面積を消費することになる。そのため、低価格の小規模FPGAにはFFT処理を実装できない場合が多い。
しかし、特定の周波数成分だけが必要な場合には、通常のFFTのように全周波数スペクトルを計算する必要はない。筆者らは、この点に着目し、DFT(離散フーリエ変換)をリアルタイム処理に適した形にして、小さな回路面積で実現できるフーリエ変換回路を考案した。
DFTでは、式1のように、N個の時間軸連続データをN/2+1個(0〜N/2番目)のフーリエ周波数成分に分解する。ここでXはフーリエ係数、kはそれに対応する周波数。xは時系列の入力信号であり、そのデータの個数はN(0〜N−1番目)である。
単一周波数成分のフーリエ係数を式1により求めたい場合でも、通常は、実数部、虚数部について、それぞれN回の積和演算を行う必要がある。しかし、次のように考えれば、リアルタイム処理に適した形にすることが可能だ。
i番目とi+1番目(時系列順)のフーリエ係数は、式2のように表すことができる。これらの式から、隣り合うフーリエ係数の差を、それぞれの積和演算を展開して計算すると、式3のように表せる。
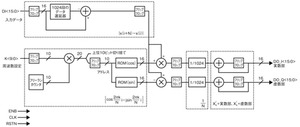
図1に示したのは、式3に基づいて作成したフーリエ変換回路のブロック図である。ここでは、入出力データのビット幅を16、時間軸連続データの数Nを1024としている。また、図中には式3との対応も示してある。
1024段のデータ遅延器はブロックRAMで構成してもよいし、LUT(Look Up Table)で構成してもかまわない(LUT領域をシフトレジスタとして使用できるデバイスに限る)。また、ROM(cos)、ROM(sin)は、それぞれcosデータ、sinデータを格納するROMである。いずれも、1/4周期分だけを格納し、アドレスの指定に応じてデータの符号変換を行う機能と、読み出し位置を逆にする機能を設けることにより、ROM容量の削減を図ることができる。
表1に、図1の回路の規模を示した。ターゲットとするデバイスは米Xilinx社の「Spartan-3E」とし、開発ツールのMAP機能を実行した結果を示している。レイアウトオプションはすべてデフォルト、ビット幅は16でNは1024とした。N段のデータ遅延器、ROM(cos)、ROM(sin)には、ブロックRAMを使用している。また、比較のために、Xilinx社が提供しているFFT用のIPの回路規模も併記している。このデータは、『DS260 Fast Fourier Transform v4.1』から引用している。表1を見ると、リアルタイム処理を行うパイプライン型と、非リアルタイム処理のバーストI/O型のいずれよりも、図1の回路のほうが面積が断然小さくなることがわかる。
このように、対象周波数が単一であれば、DFT構成をとることでフーリエ変換回路の面積を削減できる。また、対象周波数が単一ではなく数個程度である場合には、ROM(cos)、ROM(sin)のアドレス生成を少し工夫することで、リアルタイム処理に対応することが可能になる。なお、解析の対象とするのが全周波数領域の場合、リアルタイム処理には対応できないものの、一定の間隔でk(解析の対象とする周波数の設定)をスキャンする方法をとることにより、図1をベースとした回路構成でも対応が図れる。
Copyright © ITmedia, Inc. All Rights Reserved.