発散性指数関数を利用したデジタルPGA:Design Ideas
A-Dコンバータを利用する際、入力信号の振幅を調整する手段を設けていないと、小振幅の信号に対しては変換精度が劣化してしまうことがある。一方、A-Dコンバータのダイナミックレンジを超えるような大振幅の信号は飽和してしまい、本来の信号成分が失われた状態で変換が行われてしまう。このように、入力信号のダイナミックレンジが広い場合に起きる問題には、デジタルプログラマブルゲインアンプ(以下、DPGA)を使用することで簡便に対処できる。
一般に、DPGAは、オペアンプ回路のフィードバック経路に乗算型D-Aコンバータを挿入することで実現されている。この方式の場合、乗算型D-Aコンバータへの入力コードによって、アンプ回路の閉ループゲインが決まる。例えば、米Linear Technology社の「LTC6910」、あるいは米National Semiconductor社の「LMP8100」など、一般に入手可能なモノリシック型DPGAには、この構成が用いられていることが多い。
しかし、このようにデジタルコードによってゲイン(増幅度)を制御する方法では、使い勝手が悪いケースがある。また、DPGAの出力範囲に制限があり、その出力を受ける側のA-Dコンバータの入力範囲が±10Vであるといった条件に整合しないことがある。加えて、この方式の製品には、ゲインの刻みが粗く、細かい設定が行えないものが多い。さらには、消費電力が多いことが問題になるケースもある。こうした問題を回避できるものとして、本稿では発散性指数関数を利用するDPGAを紹介する。
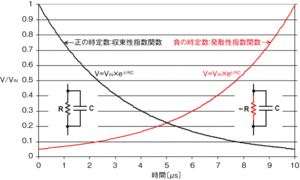
まず、収束性指数関数について考えてみる。収束性指数関数の例としては、RC(抵抗、コンデンサ)回路の放電特性が挙げられる。RC回路の両端の電圧V(t)は、電圧の初期値VINを用い、以下の式で表すことができる。
V(t)=VIN×e−t/RC (1)
この特性は、電気/電子回路技術者にはおなじみのものだ。
ここで、時間Tを以下のように定義したとする。
T=RC×loge2 (2)
そうすると、RC回路の両端の電圧は、時間TではV(T)=VIN/2、時間2TではV(2T)=VIN/4、時間3TではV(3T)=VIN/8となる。
この関数に比べると一般的ではないが、アクティブ回路で構成した負性抵抗(Negative Resistance)によってRC回路の抵抗を置き換えると、その回路の動作は発散性指数関数で表すことができる(図1)。抵抗Rを負性抵抗−Rで置き換えると、RCの時定数は負の値、つまり−RCとなる。そして、回路両端の電圧V(t)は以下の発散性指数関数で表される。
V(t)=VIN×et/RC (3)
この関数は0には収束せず、時間TではV(T)=2VIN、時間2TではV(2T)=4VIN、時間3TではV(3T)=8VINといった具合に、理論式上は無限大に発散する。すなわち、nを自然数、T=RC×loge2とすると、V(nT)=VIN×2nと表すことができる。ここで、式(3)に立ち戻って一般化すると、入力信号レベルVINがいかに小さくとも、電圧Vを得たいなら、以下の式で表される時間tだけ待てば、所望の電圧Vを得ることができるということである。
t=T×log2(V/VIN) (4)
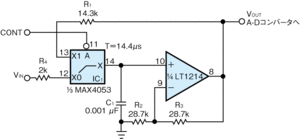
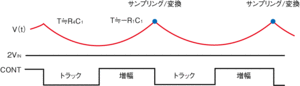
本稿で紹介する方式の基本要素は、上述した発散性指数関数と負の時定数だ。この方式を実現するものが図2の回路である。この回路は、CONT信号によって制御する。このデジタル信号がハイのときに増幅動作、ローのときにトラッキング動作となる(図3)。同信号がハイのとき、この回路はゲインが2の非反転増幅回路として働く。このとき、−(R1+RON)×(C1+CSTRAY)という負の時定数が決まる。この式で、RONはCMOSスイッチIC1(米Maxim Integrated Products社製の「MAX4053」)のオン抵抗、CSTRAYはコンデンサC1の周辺に存在する寄生容量である。ここでは、実際の負の時定数が−14.4〔μs〕であるとしよう。
時定数が−14.4〔μs〕であることから、式(2)より、T=10〔μs〕と近似することができる。式(4)ならびに、アンプ回路がゲインが2の非反転増幅回路として働くことから、この回路の入出力特性は、以下の発散性指数関数で表せる。
V(t)=VIN×2(t/10〔μs〕+1) (5)
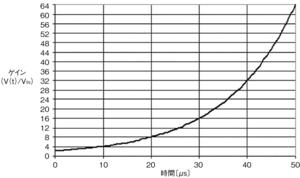
つまり、ゲインは2(t/10〔μs〕+1)で表されることになる。時間分解能を1μsとすると、増幅回路のゲインの最小ステップは1.07≒0.6dBとなり、10倍(20dB)のゲインを33ステップで刻むことができる。図4に、CONT信号がハイになってからの時間の経過と電圧ゲインの関係を示しておく。
本稿で紹介した回路はモノリシック型のDPGAとは異なり、オペアンプやスイッチなどのディスクリート部品で構成している。そのため、部品と電源電圧を適切に選定することにより、負入力や最大10Vといった入出力条件に容易に合致させることが可能だ。
アンプ回路のゲインの精度は、発散性指数関数の時定数の精度や、A-Dコンバータのサンプリングタイミングなどによって決まる。時定数の−14.4μsという値に注目すると、CONT信号に1nsの誤差があると、約0.007%のゲイン誤差が生じることになる。なお、本稿では説明を割愛するが、回路のアナログ部分の特性によって決まるゲイン設定精度を低下させることなく、使用するRC部品に対する所要精度を緩和させる方法としては、自己校正機能を組み込むことが考えられる。
Copyright © ITmedia, Inc. All Rights Reserved.