部品の誤差は何に効くのか?:抵抗/コンデンサ/コイルの基本を学ぶ(1)(1/2 ページ)
アナログ信号処理回路では、使用個所によっては、抵抗、コンデンサ、コイルの特性/仕様が直接、システムの特性/精度に影響を及ぼすことがある。また、これらの部品の選択を誤ると、予期せぬトラブルに遭遇するケースもある。本稿では、抵抗、コンデンサ、コイルそれぞれの基本特性について解説するとともに、実際のアプリケーションにおける部品選択のポイントを4回にわたって紹介する。その1回目となる今回は、抵抗、コンデンサ、コイルの誤差が回路へ及ぼす影響について検討する。
アナログ回路では誤差に注意
すべての電気/電子回路では、能動デバイスであるトランジスタやICとともに、基本的な受動素子である抵抗、コンデンサ、コイル(インダクタ)が当たり前のように用いられている。前書きでも触れたように、特にアナログ信号処理回路では、抵抗、コンデンサ、コイルそれぞれの特性がシステムの性能に直接的に影響を及ぼすことがある。また、部品の選択を誤ると、思わぬ問題を発生させてしまうこともある。
こうしたことの多くは、回路の基本要素である抵抗値R、キャパシタンス1/jωC、インダクタンスjωLが製品ごとに異なることや、その使用条件によって、ほかの要素が加わることによって発生する。ここで言うほかの要素とは、抵抗であれば主に抵抗値の誤差と許容電力、コンデンサであれば等価直列抵抗(ESR:Equivalent Series Resistance)や誘電正接(tanδ)、コイルであればQ値などが該当する。今回は、まず、抵抗、コンデンサ、コイルに共通して存在する定格値の精度/誤差が回路に及ぼす影響について検討する。
周知のとおり、抵抗、コンデンサ、コイルなど受動部品の製品ラインアップは、特殊なものを除き、JIS規格で定められたE6、E12、E24、E96などのE系列標準数列にのっとって値が定めれている(表1)。抵抗については、E96系列の高精度品も存在するが、コンデンサやコイルは、その製造技術の都合と回路設計における需要から、E12またはE24系列のものが一般的である。
ロジック/デジタル系回路における抵抗やコンデンサには、それぞれの値に対して高い精度が要求されることはあまりないと言える。それに対し、リニア/アナログ回路においては、その基本特性や値の精度が直接、回路の性能に影響するものが多く存在するため、慎重に検証する必要がある。
増幅回路では抵抗誤差はゲイン誤差に
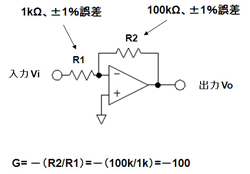
最も簡単な例として、オペアンプを用いた反転増幅回路(100倍増幅)における抵抗の誤差と回路のゲイン誤差との関係について説明する。図1に示したのは、単純な反転増幅回路である。この回路のゲインGは、R1の入力抵抗、R2の帰還抵抗の値を用いて、以下の式で求められる。
G=−(R2/R1)=−(100k/1k)=−100
より正確に言えば、オペアンプ自身のゲインが有限であることも影響するのだが、ここではオペアンプは理想的なものだとして、外付け部品である抵抗の誤差のみに着目して誤差を検証してみる。仮に、R1、R2ともに、値に±1%の誤差があるとすると、+方向の最大ゲイン誤差G+は以下のようになる。
G+=(101k/990)=102.02
すなわち、誤差分ε+は+2.02%である。
これをデシベル(dB)換算で書くと、以下のようになる。
G+(dB)=20log(101k/990)=40.17〔dB〕
つまり、誤差分ε+(dB)は+0.17dBである。
同様に、−方向の最大ゲイン誤差G−は以下のように記述できる。
G−=(99k/1.01k)=98.02
すなわち、誤差分ε−は−1.98%である。
デシベル換算では、以下のようになる。
G−(dB)=20log(99k/1.01k)=39.83〔dB〕
誤差分ε−(dB)は−0.17dBである。
このように、抵抗値の±1%の誤差は、回路のゲインに対して約0.2dBの誤差を与える。ゲイン100に対する102.02と98.02という値と、%単位での誤差、dB単位での誤差という表記の違いによって、誤差の大きさに対して異なる印象が感じられるが、実体としては同一である(アプリケーションに応じて、誤差の表記法としてどれが適しているのかという判断も併せて必要となる)。
アナログ回路において、抵抗の精度(誤差)は、その回路の精度に直接影響することになる。抵抗については、E96系列に代表されるように、1%精度の製品が用意されていることも、このような理由から来ている。
容量値の誤差は周波数特性の誤差に
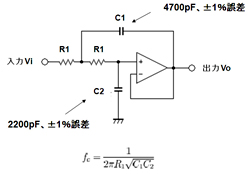
図2に示したのは、一般的なバタワース型2次LPF(低域通過フィルタ)回路である。この回路において、抵抗とコンデンサの値は、回路のゲイン、カットオフ周波数fc、Qを決定する要素となる。ここで、コンデンサの容量値のみに着目すると、その誤差は、フィルタとしての基本性能である周波数特性/カットオフ周波数にいちばん多くの影響を及ぼす。この回路おけるカットオフ周波数fcは、次式で求められる。
fc=1/2πR1√C1C2
ここで、R1=1kΩ、C1=4700pF、C2=2200pFとすると、カットオフ周波数fcは以下のようになる。
fc=1/2π×1kΩ×√4700pF×2200pF=49.495kHz
抵抗の誤差と同様に、コンデンサC1、C2それぞれについて最大1%の誤差を持つとすると、C1、C2ともに+1%の容量誤差がある場合、カットオフ周波数は以下のようになる(計算式は省略)。
- カットオフ周波数fc+:49.004kHz
- 誤差Δ:−491Hz
- 誤差率:+0.99%
また、C1、C2ともに−1%の誤差がある場合には、以下のようになる。
- カットオフ周波数fc−:49.995kHz
- 誤差Δ:+500Hz
- 誤差率:1.01%
これらの結果は、誤差要因にはC1とC2の2つが存在し、それぞれが最大1%の誤差を有していても、カットオフ周波数fcの誤差は単純な足し算による2%ではなく、約1%になるということを意味している。増幅回路における抵抗の誤差とゲインの誤差との関係に比べて、コンデンサの誤差がフィルタ回路の周波数特性に与える影響は約1/2である。過去からのこうした検証の積み重ねにより、抵抗とコンデンサの製品ラインアップにおいて、使用する標準数列が異なるという結果となっていると言える。
なお、ここでは、フィルタ回路においてコンデンサの誤差が回路に影響を及ぼす例を示したが、このように、回路の特性を決める用途以外では、容量値として高い精度は求めないことが一般的だ。例えば、電源デカップリングの用途や、ACカップリングなどの用途などでは、容量値について高い精度は要求しないということである。
Copyright © ITmedia, Inc. All Rights Reserved.
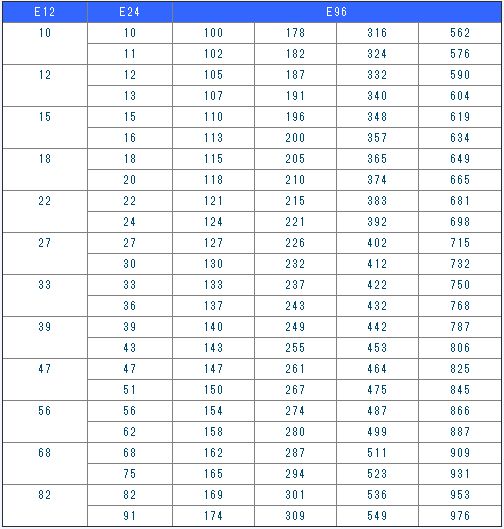 表1 E系列の標準数列
表1 E系列の標準数列