Spiceの応用解析――微分方程式を解く:SPICEの仕組みとその活用設計(22)(1/4 ページ)
今回は数値計算の代表的なツールであるSpiceの応用解析として、“アナログコンピュータ”を模擬して代表的な微分方程式を解いてみます。
アナログコンピュータ
現在では“コンピュータ”と言えばデジタル方式を指すことが当たり前となっていますが、“デジタル”方式が一般化する前の1950〜1960年代はコンピュータと言えばアナログ方式を指していました。当時のアナログコンピュータは解の連続性という特徴を活かして主に微積分方程式や種々のシステムの自動制御の応答問題を解くことに活用されていました。
そして、“デジタル”方式が普及するにつれて区分するために“デジタル”方式に対比してアナログ方式と言われるようになっていくのです。
やがて“デジタル”方式が広く使われるようになるとアナログ方式は廃れていくのですが、今でも“オペレーショナル・アンプ”、いわゆる”オペアンプ”の名前にその面影を見ることができます。
オペアンプ=演算増幅器は方程式を解く過程の四則演算や微積分演算を担当する回路として発達したのがその名前の起源です。
その特徴は数学的近似を成立させるために“利得はできる限り大きく”、“入力インピーダンスはできる限り高く”、“出力インピーダンスはできる限り小さく”、という点にあり、これらの特徴は今でもオペアンプのカタログに記載されている特性項目です。
このような発展の歴史から今でも高利得・低出力インピーダンスの差動入力型の増幅器が“演算増幅器”と呼ばれているのです。
今回は数値計算の代表的なツールであるSpiceの応用解析として、このアナログコンピュータを模擬して代表的な微分方程式を解いてみます。
1階の微分方程式を解く
例えば指数関数として有名なeについて考えます。数式で書けば次のようになります。
Y'=Y …1式
この関数の定義としては「Yの微係数の値Y'はYに等しい」ということです。
しかし、この定義だけでは解が存在するのか否か、また解が存在する場合でも解の形状や具体的な値を想定するのは解の様子を俯瞰(ふかん)できる曲線などがなければとても想像できるものではありません。
その点、アナログコンピュータは解として曲線を出力してくれるので初心者にとって解の様子をイメージする手助けになることは間違いありません。
では実際にアナログコンピュータでこの1式を解いてみましょう。
まず、1式のYとY'の関係ですが、言葉で書けば“Yの微分出力=Y”です。
しかし、信号に含まれるノイズ成分を微分すると出力に大きなノイズが発生して各部が飽和することになります。また、“微分回路=ハイパスフィルタ”ですから微分回路を通すたびに信号の高周波成分が強調されるので正しく演算するには演算増幅器の大振幅周波数特性が高域まで延びていることが必要になりますが、この特性を実現することは実際には不可能です。
ですから、アナログコンピュータで微分回路を使うことはあまりなく、ローパスフィルタに相当する積分回路で等価になるように工夫します。
1式を積分すると積分定数をCとした2式になります。
つまり、2式に従えば積分器の出力=積分器入力となるように回路を構成すれば良いことになります。具体的には図1のように積分器の入出力を短絡する形になります。
(ここではPSpiceの積分器(INTEG)を使用します)
2式において、
です。したがって積分器の初期値CがY'とYの初期値ということになります。
また、Y'=YですからC=0とすると、Y'=0となって微係数が0になり、かつY'=Y=0ですから原点を通ります。そして、この曲線は微小時間Δtだけ経過しても微係数は0ですからYの値は0を維持します。
結局、C=0の時は時間軸を示すことになります。
(Y=t2のような場合、Y'=2tですから微係数はtの値と共に増減しますが、今回はY'=Y=0ですから傾斜は変化できません)
これも解の1つですが初期値を0以外に設定した場合にはどうなるでしょうか?初期値Cとして有限な値を設定して図1の回路で仮解析してみると解としては指数関数の形状を採ることが分かりました。一般解としては
Y=α・βt=C・eat …3式
です。
3式を1階微分して1式と比較するとa=1でなければなりませんし、積分定数Cは関数の係数になりますので関数の基本形としてa=1,C=1とします。そしてこの場合のeの値をネイピア数、あるいは自然対数の底と言います。
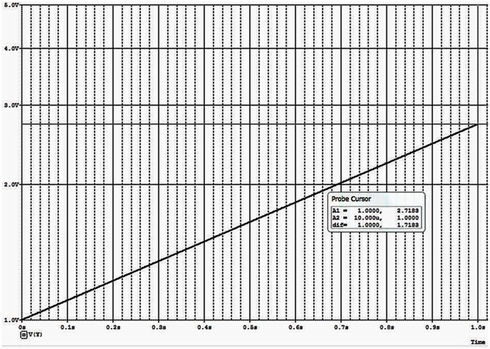
これで2式を実行できる条件がそろいましたので図1に示す回路で実行(TimeStep=1ms)し、その結果を図2に示しますがきれいにEXP波形が再現されています。
ネイピア数としてのeの値を求めるためにt=1の値を読み出してみるとY=2.71828198432922になり、実用上問題のない精度(誤差ε=5.7×10-8)で解を得ることができます。
当然のことながら時間刻みを粗くすると精度は低下しますが、現在のPCの能力であれば今回のような1000回程度の演算は問題にはならないでしょう。
一方、本来のアナログコンピュータは連続出力ですので時間刻みに関する問題はありませんが、読み取り精度が3桁程度でしたのでここまでの精度はありませんでした。
Copyright © ITmedia, Inc. All Rights Reserved.

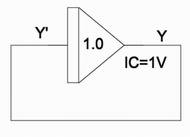 図1 2式の実行回路
図1 2式の実行回路