接続形態(トポロジ)と特性インピーダンス:高速シリアル伝送技術講座(4)(3/5 ページ)
特性インピーダンスとは?
差動ケーブルの90Ωや100Ωなどの差動インピーダンス、基板上のマイクロストリップやストリップラインの50Ωシングルエンドのインピーダンスなど、伝送路の特性は抵抗値で示されています。また、伝送路のインピーダンスに合わせて、終端部にそのインピーダンスと同じ値の抵抗を配置し信号の反射を防いでいます。それでは伝送路の差動90Ωやシングルエンド50Ωは単純にテスターで測定できる抵抗値でしょうか?
まず電気回路のインピーダンスとは交流を流した場合の電圧と電流の比率の意味で,Z0=R(純抵抗)+jX(周波数依存のリアクタンス)で表します。「90Ω差動ケーブル」「50Ω同軸ケーブル」「プリント基板の50Ωマイクロストリップライン」など伝送路のインピーダンスは抵抗値で表示されますが、実際にテスターでDC抵抗値を測定してもほぼ0Ωのため、このZ0の式から伝送路のインピーダンスはリアクタンス成分が支配的であることが分かります。また周波数が変化してもリアクタンス部は変化しません。
この伝送路の独特なインピーダンスの特性は英語で「Characteristic impedance」と呼ばれ、日本語では「特性インピーダンス」と訳されます。Characteristicの意味は特徴、特質で、ケーブルなどの伝送路はこの特有なインピーダンスを持っているという意味になります。
ここでは伝送路の特性インピーダンスはリアクタンス成分が支配的であること、周波数や長さに依存しないことを従来の伝送路のLCR等価回路からのマクロ的な説明と、電磁気学の電界と磁界を基とした、形状と比誘電率の考え方の両方を説明していきたいと思います。皆さん比較してみてください。
LCR等価回路での特性インピーダンスの説明
インピーダンスとは純抵抗Rの実数部とリアクタンス成分の周波数(角速度)に依存するLとCの虚数部で表現され、それぞれを足したものがインピーダンスになります。LCR直列回路では,図11のZ0式になります。
R、L、Cの直列回路のインピーダンスは、純抵抗成分Rと、虚数部の角速度(周波数)を係数とするリアクタンス成分j[ωL−1/ωC]の合計で、同軸ケーブルや基板のストリップラインの伝送路も、電気回路で表現できるインピーダンス特性を持っていることが分かっています。同軸ケーブルやストリップラインはコンデンサー、インダクター、抵抗など電子部品は入っていませんが、電気回路として特性を近似するとマクロ的には図12のLCRG等価回路になります。
この近似のLCRG伝送路等価回路の表現は実測での高周波帯域のSパラメーターやエッジレートの速いTDR(タイムドメインリフレクトメトリ)で時間軸のインピーダンス解析では高周波領域の再現性が低く、ミクロ的な解析のために分布乗数としてどの程度細かく分けるかの論議になったりもしますが、伝送路を伝わる高い周波数の信号は、実際はGNDと信号線間や差動信号間の電磁気的な電界、磁界の結合で伝達しています。伝送路のLCRG回路はあくまでマクロ的な表記になりますが、伝送路の特性インピーダンスの特徴を、まずLCGR等価回路の考え方で説明していきます。
図12のLCRGで示したケーブル等価回路の単位長当たりのインピーダンスZ0は、周波数依存(ω=2πf)の角速度jωの係数を持ち、以下の式で表現できます。
分母のjωCは周波数依存のキャパシタンス、分子jωLは同様に周波数依存のインダクタンスです。ここで導体損失のRと誘電体損失のGは、このjωL、jωCと比較して十分に小さいため無視します。
また分母、分子の周波数依存のjω(ω=2πf)は共通項で消去できます。結果、単位長さ当たりのインピーダンスはZ0≒√(L/C)となり、リアクタンス成分(インダクタンスとキャパシタンス)のLとCで単純に表現可能となりました。このことから、伝送路の特性インピーダンスは周波数に依存しないことが分かります。
次に、伝送路の長さをaとし、ケーブルのインダクタンスの合計をa×L、キャパシタンスの合計をa×CとするとZ0≒√(aL/aC)となり、分母と分子の長さaが消去され同じようにZ0≒√(L/C)となります。
よって特性インピーダンスは長さにも関係ないことが分かります。
同軸ケーブルやストリップラインなどの単一な構造の伝送路ではLとCの比率が一定で、特性インピーダンスは周波数と長さに依存しないことが分かりました。LとCの値があれば実際の特性インピーダンスを求めることができます。
これは電界と磁界が直交して伝搬するTEM(Transverse Electro-Magnetic)波で信号が伝送すると考える同軸ケーブルや並行板、ストリップライン構造のシンプルな単一構造体が該当します。
図13は電界と磁界が直交しながら電磁波(TEM波)が空間を伝搬する様子を表していますが、導体での伝送路中の変化する信号は、まず伝送路に電位差があると図14の赤矢印の電界が生じ、その電界に直交した水色の磁界が発生します。磁界が変化すると導体に電磁誘導により起電力が生じ、また電界が発生します。この電界と磁界の相互の誘導作用の関係で、同軸ケーブルやストリップラインでは信号が伝達すると説明できます。
Copyright © ITmedia, Inc. All Rights Reserved.
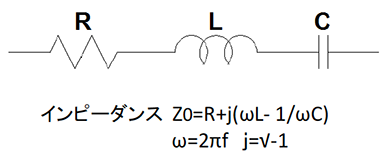 図11:LCR直列回路
図11:LCR直列回路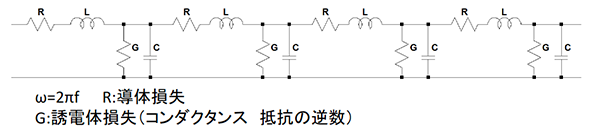 図12:伝送路のLCRG等価回路
図12:伝送路のLCRG等価回路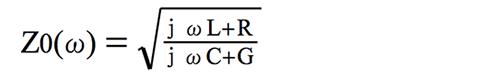
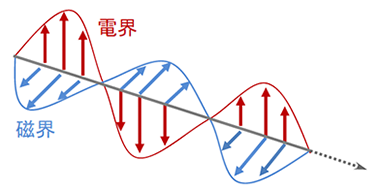
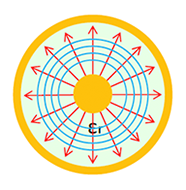 左=図13:電磁波(TEM波)の伝搬、電界と磁界の相互関係、右=図14:同軸の電界と磁界
左=図13:電磁波(TEM波)の伝搬、電界と磁界の相互関係、右=図14:同軸の電界と磁界