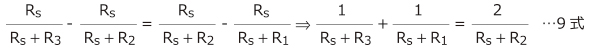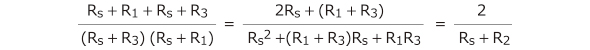サーミスタ(3) ―― NTCサーミスタによる温度検出回路:中堅技術者に贈る電子部品“徹底”活用講座(13)(3/4 ページ)
NTCサーミスタの応用例
サーミスタの応用を考える前に各種回路への適用検証が可能なようにSpiceを用いてNTCサーミスタの特性を表すことを考えます。
サーミスタは、自己発熱がないものとすれば1式で表されるような温度係数を持つ抵抗素子と考えることができます。
この考え方からNTCサーミスタの温度特性をシミュレーター上で再現するには抵抗値の温度係数の項に1式の特性を代入すればよいことになります。図1は、B定数3434K、Rb=10KΩ(25℃)の定数を使ったサーミスタの温度特性のシミュレーション回路例です。
Spiceの解析コマンドとしてLT-spiceの例を示しますが他のspiceでも同様の構文で解析可能です。
.step temp 開始温度 終了温度 刻み
.op
このようにして行った温度特性のシミュレーション結果を図2に示しますがNTCサーミスタの特性をうまく再現されていることが確認できます。
NTCサーミスタによる温度検出
NTCサーミスタは高温でRtが小さくなり、図3のように分圧回路の上段に用いた場合に検出信号Eoは高温で上昇します。
つまり、温度〜検出電圧は正の関係を持ちますのでこの原理を用いてNTCサーミスタで温度を検出することができます。
ただし、Rtは温度に対して図2のような非線形特性を持ちますので、検出抵抗Rsを変えるとEoのうねり具合は変化し、Rsの値には直線性に関する最適値があることが分かります。
ここでは計算を簡単にするために温度は等間隔な次の3点とし、この3点が直線上に並ぶものとします。したがって、
T1:Eo=E1,Rt=R1
T2:Eo=E2,Rt=R2
T3:Eo=E3,Rt=R3
T1<T2<T3、でありΔT32=(T3−T2)=ΔT21=(T2−T1)とした時、
(E2−E1)=(E3−E2)です。
これらの関係を式で表せば次の8式のようになります(Esは分圧回路への印加電圧)
等間隔な測定点3点が直線上に並ぶということはそれぞれの検出信号の差分も等しいので次の式が成立します。
9式をRsについて解いて次の結果を得ます。
右側の等式を解いて、
Copyright © ITmedia, Inc. All Rights Reserved.
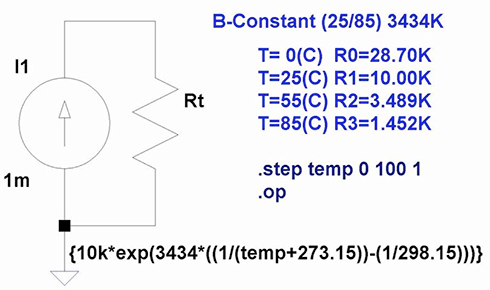 図1:サーミスタの温度特性測定回路
図1:サーミスタの温度特性測定回路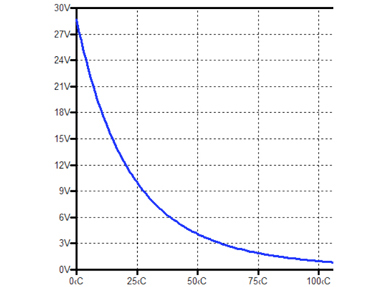 図2:Rtの温度特性
図2:Rtの温度特性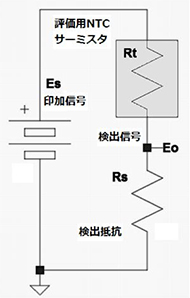 図3:温度検出回路
図3:温度検出回路