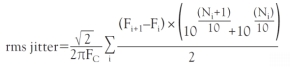ジッタと位相ノイズの測定にPLLの分周器を活用:目指せ“パーフェクトタイミング”(2/3 ページ)
分周の影響を評価する
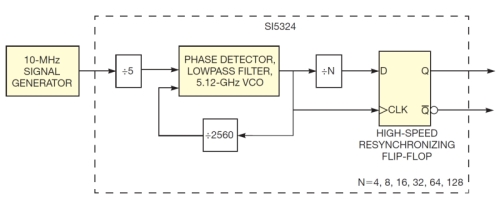
以下では、具体的な例として分周比を2の累乗(4、8、16、32、64、128)に設定し、位相ノイズと位相ジッタの両方に与える影響について説明していく。これらの測定では、Silicon Laboratories(シリコン・ラボラトリーズ)のPLL IC「Si5324」を使う(図5)。PLL ICの最終的な出力クロックの周波数に関わらず、高速VCOが出力クロックに同期していることに留意してほしい。つまり、クロックエッジの形状とタイミングは、分周比を変えても同じなる。唯一の違いは、分周比を高めると一定の時間に生じるクロックエッジの数が減っていくという点だけだ。リタイミングに起因するノイズがある程度は残ってしまうものの、その大きさは全ての分周値に対して同じである(図6)。
図6に示した6本のカーブは、それぞれPLL ICの分周比を4、8、16、32、64、128の6通りに設定したときの位相ノイズ特性である。カーブ同士は、縦軸方向で6dBc/Hzずつ互いにずれているものの、形状自体は6本とも基本的に同じだ。縦軸方向の6dBのずれは、わずかに例外的な部分はあるが、それを除けば横軸(オフセット周波数)の値が変わっても、分周比が変わっても常に一定である。
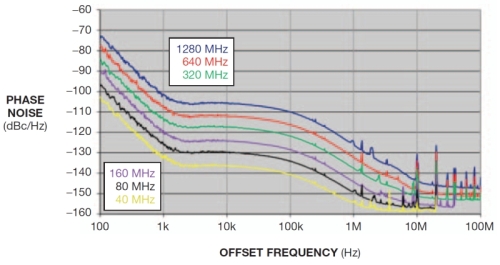 図6 PLL ICの最終的な出力クロックの周波数に関わらず、高速VCOが出力クロックに同期している。つまり、クロックエッジの形状とタイミングは、分周比を変えても同じなる。唯一の違いは、分周比を高めると一定の時間に生じるクロックエッジの数が減っていくという点だけだ。
図6 PLL ICの最終的な出力クロックの周波数に関わらず、高速VCOが出力クロックに同期している。つまり、クロックエッジの形状とタイミングは、分周比を変えても同じなる。唯一の違いは、分周比を高めると一定の時間に生じるクロックエッジの数が減っていくという点だけだ。ただ、オフセット周波数が最大になる図の右端の領域では、カーブ同士の縦軸方向の間隔は圧縮されており、圧縮の度合いは分周比が高まるほど大きくなる。つまり分周後のクロック信号の周波数が低くなるほど、縦軸方向のカーブ同士の間隔は狭くなっている。このような現象が起きる理由はこうだ。すなわち、この位相ノイズの測定器として利用したAgilent Technologies(アジレント・テクノロジー)のシグナルソースアナライザ(SSA)「E5052B」のノイズフロアが、PLL ICであるSi5324の位相ノイズの値に近いからである。このようにノイズフロアが問題になるのは、ジッタが極めて低いSi5324を使いながら、分周比を高く設定して出力クロック信号の周波数が低くなるからだ。
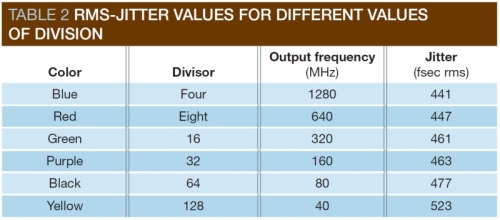
表2に、6通りの分周比それぞれについて、100Hz〜20MHzの範囲でジッタを積分した結果を示した。出力クロックの周波数が低下するにつれて、ジッタがわずかに増大しているだけだという点に注目してほしい。これは、分周比が変わると位相ノイズは6dBずれるにもかかわらず、出力ジッタが相対的に一定であるという証拠である。分周比を高めて出力周波数が低下した際にジッタが増大する度合いは、分周比が高くなるほど(出力高周波数が低くなるほど)より顕著になる。この位相ノイズの増加には、測定器のノイズフロアとエイリアシングという2つの要素が起因している。これらについて考察を進めよう。
ノイズフロアと位相ノイズ
ジッタが非常に小さく、周波数が低いクロック信号では、測定器のノイズフロアが位相ノイズの測定限界を決める要因になる可能性がある。測定限界を超えてしまうと、そこではDUTの特性ではなく、測定器の特性を見ていることになってしまう。先ほど確認したように、クロックの周波数が低下するにつれて位相ノイズは単調に減少していくが、クロックエッジのrmsジッタはほぼ一定値のまま変わらない。位相ノイズを積分してrmsジッタを求める際に、その同じクロック周期を用いるからだ。
もう少し詳しく、例を使って説明しよう。rmsジッタの値を求めるために位相ノイズを積分するプロセスを追ってみる。最新型の位相ノイズ測定器は一般に、測定結果をCSVファイル(コンマ区切りのデータ列ファイル)として出力する。このファイルには2列のデータ格納されており、1つはクロック周波数からのオフセット周波数(単位はHz)で、もう1つはそのオフセット周波数における1Hz当たりの位相ノイズ(単位はdBc/Hz)だ。これらのデータを組み合わせれば、特定のオフセット周波数における位相ノイズが分かる。
この積分は次のような手順で進める。まず、各オフセット周波数ポイントにおける位相ノイズの大きさを、線形値=10(dBc/Hz)/10という式を使って線形化する。次に、全オフセット周波数ポイントをつなぐカーブの下側部分の面積を求める。
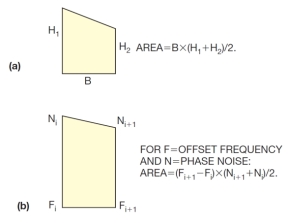
2つの隣接する周波数ポイントが作る台形の面積を計算するには、図7に示した式を使う。
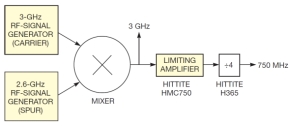
こうして全ての台形の面積を求めて合計すれば、カーブの下側部分の面積が得られる。最終的なrmsジッタの値を求めるには、2つの係数でスケーリングを掛ける。1つは、√2という定数である。この値を用いる理由は、位相ノイズの測定では単側波帯(SSB:single side band)だけを測定しているのに対し、rmsジッタは両側波帯(DSB:double side band)で考えるからだ。通常、位相ノイズの2つの側波帯は、クロック信号の周波数を挟んで対称性を有すると見なせる。また、ここで取り上げた事例ではリミットアンプを使っており、それが振幅変調(AM)を抑制して周波数変調(FM)を通過させることから、2つの側波帯の対称性はさらに確実になる(図8)。
もう1つの係数は、積分した面積の単位を変換し、単位間隔(UI:unit interval)ではなく時間の単位でジッタを表わすためのものだ。この係数を掛けると、rmsエッジジッタ値は相対的に一定に保たれる一方、位相ノイズ値は変化する。rmsジッタを求める式は、最終的に以下のように表される。
ここで、Fcはクロック周波数、Fiはi番目のオフセット周波数ポイント、Niはそのポイントにおける位相ノイズ(cBc/Hz)である。
Copyright © ITmedia, Inc. All Rights Reserved.