SPICEモデルとライブラリ(その1):SPICEの仕組みとその活用設計(10)(2/3 ページ)
デバイスモデルとは
デバイスモデルとは、素子の特性を等価回路で再現したもので、SPICEモデルの考え方の根源を成しています。例えば、バイポーラトランジスタでよく用いられるモデルとしてはエバース・モル(Ebers-Moll)モデル、ガンメル・プーン(Gummel-Poon)モデルが有名です。
デバイスモデルの例として、本連載の第3回「ダイオードなどの非線形負荷を節点法で解析する」で紹介した、ダイオードの基礎的方程式としてのショックレーのダイオード方程式を式(1)として再掲します。
ここで、Ifはダイオードの順方向電流、Vfは順方向電圧、Isは逆漏れ電流、Vtは熱起電圧です。
この式は理想ダイオードの式なので、例えばIsに10−14Aを与えた場合の順方向特性は図1のようになります。
一見するとダイオードの特性を表しているように見えますが、片対数グラフを使って、実際のダイオードの順方向特性と比較してみると、図2の破線と実線のように差異があることが分かります。
この差異が生まれる原因はいくつかあります。例えば、図3(a)のような理想状態のダイオードに仕上げることができない製造上の限界や、式(1)で考慮できなかった要素、使用するシリコンウエハーの品質などにより、実際の構造は図3(b)のようになってしまいます。
表1に、ダイオードの理想モデルと実際の構造の差異を簡単にまとめておきました。
しかし、SPICEが実際に使用する数学的モデルにおいては、図4のように、これらの差異を数式で表現できるように考慮されています。
例えば、Rsを考慮すると、実際のPN接合に働く電圧Vfは(Rs×If)だけ低下しますから、式(2)や式(2’)となります。
この式(2)をVfについて解くと、
となります。
また、Isを今までは一定値として扱いましたが、実際には式(3)のように温度(T)、エミッション係数(N)、温度指数(XTI)などに依存した特性になっています。
ここで紹介したこれらの式は、係数(N、Eg、XTI、Rs、Is)を変えることで、領域ごとの曲がり具合を変えることができます。このため実際の曲線に合致するように各係数を選択・調整すれば、実際の半導体の特性を模擬できるようになります。
このように、素子のタイプごとに数式の型が決まってるからこそ、微分コンダクタンスの数式もあらかじめ決めることができ、素子の種別を指定することで回路要素行列[G]へ機械的に組み込むことができるわけです。
Copyright © ITmedia, Inc. All Rights Reserved.
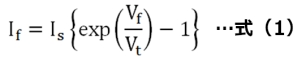
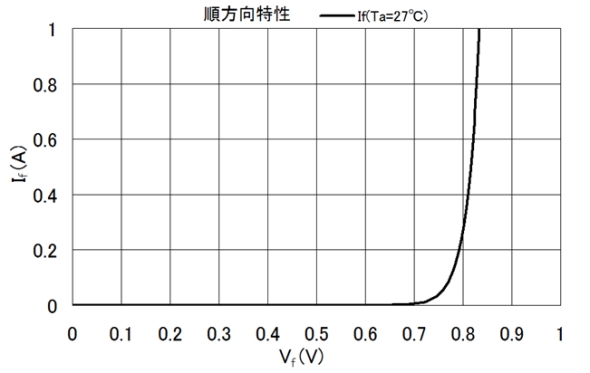 図1 ダイオード順方向特性の計算結果
図1 ダイオード順方向特性の計算結果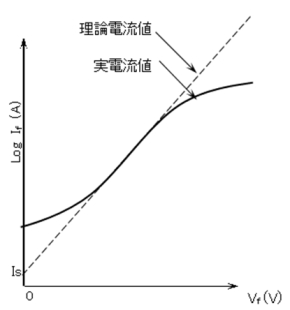 図2 理論特性と実電流特性
図2 理論特性と実電流特性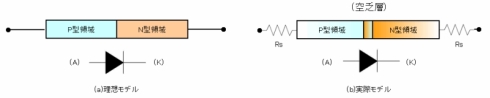
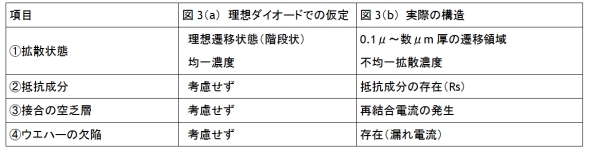 表1 ダイオードの理想モデルと実際の構造の差異
表1 ダイオードの理想モデルと実際の構造の差異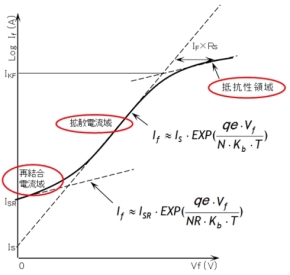
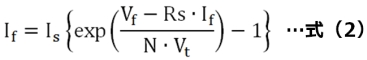
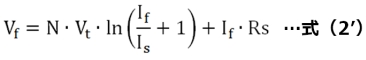
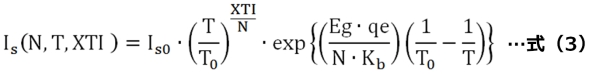
 式(3)の係数の説明
式(3)の係数の説明