SPICE応用設計(その3):工程能力設計:SPICEの仕組みとその活用設計(14)(3/3 ページ)
補足情報
スルーレート(Slew-Rate)
スルーレート(SR)とは一言で言えば「電圧変化率」のことで、単位はV/μSです。つまり、1μSの時間内に何V変化できるかという指数で、大振幅時の出力電圧の立ち上りのテーパーを決める因子です。この値は内部回路構成が値を左右しますが、重要なのはこの値は“負帰還を施して値を改善できるものではない”ということで、回路構成を決める段階で目標値を決めてやる必要があります。
SRは数学的には瞬時電圧V(t)を時間で微分し、その最大値をとれば良く、正弦波の場合は3式で計算できます。
今回の設計例で取り上げている設計条件のVp=4.4、f=40KHzを代入すると
となります。
1.11V/μSの値がどの程度かピンとこない人が多いと思いますが、汎用オペアンプとして有名な741型、および324型のSRが0.5V/μS程度なので2倍近く高速駆動ができる能力だということです。この値は振幅Vpに比例しますので高インピーダンスで出力の大きなアンプほど大きなSR値が要求されます。
AC解析と収束問題
SPICEで扱うトランジスタ、ダイオード、キャパシタ、インダクタンス、などの部品は計算時には電圧源、電流源、等価コンダクタンスにまで分解されて線形の回路網に置き換えられています。
AC解析ではこの線形回路網に交流信号を与え、周波数を掃引しながら任意の節点の電圧を計算しますのでAC解析には収束問題は発生しません。想定した結果と異なる場合は基本的にDCバイアスの問題になりますのでバイアス条件を見直すことになります。
(部品の等価回路については連載の第3回、第4回、第5回を参照してください)
モンテカルロ法とは
モンテカルロ法とはWikipediaによれば「シミュレーションや数値計算を、乱数を用いて行う手法の総称」とあり、数値計算の分野では方程式は作れても解くことができない場合の解を得る手法として有名です。
その中でもSPICEにおけるモンテカルロ解析は計算サイクルの都度、部品にランダムな偏差を与えて、「回路の特性がどのような分布になるか」を調べることを指しています。
なお、なぜ“モンテカルロ”と呼ぶかというと、「中性子の研究プロジェクトで付けられたコード名に由来する説(IT用語辞典e-Wordsなど)と、確率的でギャンブルのようなため、カジノの多いモナコの地名に由来するという説があります。
一様分布と正規分布(ガウス分布)
モンテカルロ解析でよく用いられる偏差の分布形状として表1で用いた一様分布と正規分布の2通りの形状があります。この2つの分布のSPICEでの扱いにはそれぞれ特徴があり、
- 一様分布:与えた偏差が上下限値
- 正規分布:与えた偏差は標準偏差(σ)
となるツールがほとんどです。
しかし一律に5%と設定した場合、一様分布では±5%の巾の中に100%が含まれる矩形型の分布であるのに対して、σを指定した正規分布では±15%(±3σ)の巾の中に99.7%が入るような釣鐘型の分布を与え、一様分布とは分布の巾自身が変わってしまいます。分布形状を変えた場合には偏差の値も変えなければならないという点に留意してください。また、正規分布はガウス分布と呼ばれる時もあります。
偏差の形状検討
表1では1KHz時のV(out)、及びV(out)のカットオフ周波数fcの分布を表示させましたが、正規分布と一様分布では分布の形状が異なっていることが分かります。どちらを採用すべきなのでしょうか?
まず、1KHz時のV(out)の偏差の様子を考えましょう。図1の回路で1KHzでの利得に影響するのはR3(600Ω 5%)、R4(20.2K 5%)だけです。
この場合の偏差は平方和で求めることができ、偏差εはε=±√(2×0.052)=±0.07です。
具体的な値としては±(4.4×0.07)Vですから幅としては0.622Vです。シミュレーションの値と比較すると、一様分布の方がより近い値を示しています。(差分はそれぞれ+14%と△27.5%)
また、カットオフ周波数fcの分布についても同様に次のように計算できます。
V(out)の場合と同様にカットオフ周波数fcに影響する定数はR4(20.2K 5%)とC1(85pF 10%)です。
平方和を採った偏差εはε=±√(0.052+0.12)=±0.112です。
具体的な値としては±99.5KHz×0.112ですから幅としては22.3KHzになります。こちらの場合もやはり一様分布の方がより近い値を得ることができています。(+15%と△21.5%)
正規分布を採用すると3/1000個は±3σの範囲外になる可能性があるのですが、実際の部品の偏差は値を検査しているのでそのような分布にはならず、結果の判定に困る場合もあります。
部品偏差の実態
モンテカルロ解析においては部品に偏差(バラツキ)を与えなければなりません。このバラツキは経験的には体に染み付いているのですが、具体的な特性値を計測したものはあまり公開されてはおらずねがてぃぶろぐさんのような一部のWebページなどに限られています。この資料には表示値10KΩ±5%のカーボン抵抗器98本の抵抗値分布の実測値が示されており、筆者の場合、最多値9.90K、Min9.825K、Max10.00Kとグラフから読み取ることができました。最大偏差は(9.825-10)/10=△1.75%です。
ただ、これは1ロットの値ですから、ロット間変動を含む定常的なバラツキとしては経験的には2倍程度を考えれば良く、実力的には±3.5%程度の偏差と考えることができます。
また、この±3.5%という値を3σ相当と考えれば部品規格としての4σは±3.5%×1.33、つまり、±4.7%、ほぼカタログ通りの偏差となります。
本連載における偏差の考え方
部品の検査工程ではさまざまな処理が行われており、その処理が偏差の形状にも影響してきます。ここでは主な手法としてランク選別とトリミング加工について考えます。
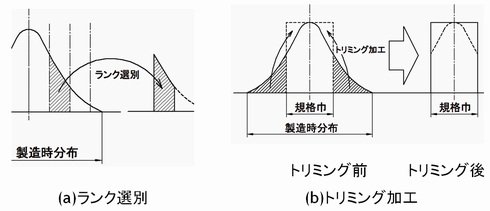
ランク選別は昔から行われてきた手法で、図5(a)のように、広い偏差を持つ部品をいくつかの細かいランクに選別するものです。同図では右下がりの分布ですが、別のロットから採った分布では逆の傾きになっている時もあり、長期間の平均を採ればさまざまな分布が重なり合って一様分布に近くなります。
また、最近のチップ抵抗であれば図5(b)のトリミング加工を標準で実施しており、合わせ込み調整がされています。
このような場合にも一様分布に近いバラツキになります。
このような背景、及び複数の一様分布の組み合わせが三角分布という現実の分布に近い形状になることを考慮して本連載では分布としては一様分布で偏差を与えることにします。
次回は今回説明しきれなかった、モンテカルロ解析の結果の応用について補足説明をしていきたいと思います。
記事訂正のお知らせ:前回のSPICE応用設計(その2):フーリエ解析において、LTspiceに関係する記述を加筆、訂正しています。
執筆者プロフィール
加藤 博二(かとう ひろじ)
1951年生まれ。1972年に松下電器産業(現パナソニック)に入社し、電子部品の市場品質担当を経た後、電源装置の開発・設計業務を担当。1979年からSPICEを独力で習得し、後日その経験を生かして、SPICE、有限要素法、熱流体解析ツールなどの数値解析ツールを活用した電源装置の設計手法の開発・導入に従事した。現在は、CAEコンサルタントSifoenのプロジェクト代表として、NPO法人「CAE懇話会」の解析塾のSPICEコースを担当するとともに、Webサイト「Sifoen」において、在職中の経験を基に、電子部品の構造とその使用方法、SPICE用モデルのモデリング手法、電源装置の設計手法、熱設計入門、有限要素法のキーポイントなどを、“分かって設計する”シリーズとして公開している。
関連記事
 SPICEモデルとライブラリ(その2)
SPICEモデルとライブラリ(その2)
必要なSPICEモデルがツールに含まれていない場合は、第三者提供のものを使う必要がある。第11回では、SPICEモデルの入手方法や、開発STEPとモデルの精度の考え方について説明する。有用なサブサーキットモデルについても紹介しよう。 SPICEモデルとライブラリ(その1)
SPICEモデルとライブラリ(その1)
設計した回路をSPICEで解析するには、使用している部品のSPICEモデルが必要だ。第10回では、このSPICEモデルについて解説する。
Copyright © ITmedia, Inc. All Rights Reserved.