SW電源の解析：SPICEの仕組みとその活用設計（最終回）（2/4 ページ）

現状の解析手法

　前述したように、SW電源の異常発振に対する安定性の検証には測定器メーカーの提案する周波数応答法(FRA法)が主に用いられていましたが、この手法は制御信号に信号を混入させて出力にどの程度反映されるかを検出するものです。ですから負帰還(制御)を掛けないと回路が安定にならず、実際に測定できるのはクローズドループ特性に限られ^＊）ていました。また、シミュレータによるFRA法としてSCATのように自動でFRA曲線を測定してくれるツールもあります。

　しかし、FRA曲線と各設計パラメータの対応が分かりづらく、設計者によってはどの部品の定数がピークを作っているのか分からないまま見当違いの素子を調整していることも時としてありました。

　このような実測を主とした面からではなく、理論的な解析から線形化モデルを得る「状態平均化法」も1980年代から使用されていますが、インターネット上の書き込みを見ると今でも状態平均化法に二の足を踏んでいる方や使いこなしに困っておられる方が多いのが実情ではないでしょうか。

　ここでは新しい測定法として、Spiceを使ったStep応答法を紹介するとともに、この手法で求めた伝達関数を状態平均化法、Spice-FRA法、及びSCATｰFRA法から求めた曲線と比較し、SW電源の線形モデル化を考えていきます。

＊）クローズドループ特性からオープンループ特性を計算する測定器もありますがノイズの分離が困難です

SpiceによるStep応答法

　SpiceによるStep応答法の考え方の概略を次に説明します。入力信号をEin(s)、伝達関数をT(s)、出力信号をO(s)とした場合、入出力の関係は1式になります。

　　　O(s)=Ein(s)×T(s) …1式

　ですから、ラプラス変換が1となるインパルス信号(δ関数)を入力信号として与えた場合は2式のように出力波形を伝達関数と見なすことができます。

　　　Ein(s)=1 ⇒ O(s)＝1×T(s) …2式

　しかし、δ関数の定義は印加時間巾t_Wが0であるにも関わらず時間積分値が1になる特殊関数で、実際に回路上で実現することはできません。例えば、パルス巾t_W=1μSとしても電圧値は10⁶Vになり、回路の線形動作はとても保証できません。

　次にδ関数の衝撃を緩和するためにδ関数を積分したもの、つまり単位Step関数を考えます。この場合の入力信号は階段状になり、実回路上でもSpice上でも実現することは容易です。しかし、実際の入力信号は時間的な傾斜を持った擬似Step関数E_SL(s)であり、周波数特性の誤差を含んでいます。
(理想Step関数はDC成分だけでAC成分を持ちませんが擬似Step関数はDC成分+AC成分になります)

　また伝達関数T(s)は入出力信号の比ですが、擬似Step関数E_SL(s)はDC成分が主でAC成分は極めて少ないので精度を上げるために少し工夫をして3式のように考えます。

　このように求めた実際の応答波形を図1に示します。この波形を3式に従って処理して伝達関数を求めれば良いのです。

＊Step応答法はSpice-FRA法に対して同じ回路図を使いながら解析時間を1/10〜1/20に短縮でき、精度も格段に良い利点があります。

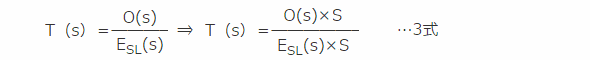
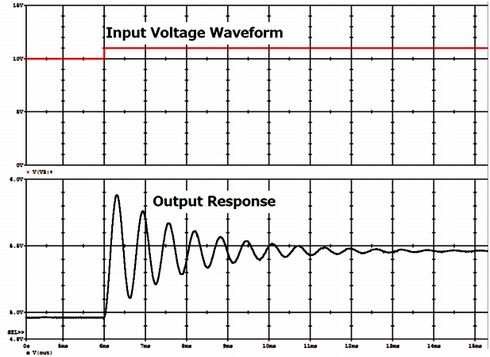図1：SW電源出力波形例(処理前) （クリックで拡大）